Coachingatyourplace: 2020

Friday, May 29, 2020

NUMBER SYSTEM

NUMBER SYSTEM

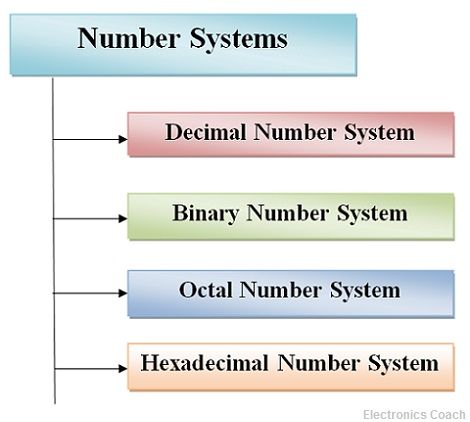
It is the mathematical notation for representing numbers of a given set by using digits or other symbols in a consistent manner.
...
The four most common number system types are:

Decimal number system (Base- 10)
Binary number system (Base- 2)
Octal number system (Base-8)
Hexadecimal number system (Base- 16)

Binary Numeral System - Base-2

Binary numbers uses only 0 and 1 digits.

B denotes binary prefix.

Examples:

10101₂ = 10101B = 1×2⁴+0×2³+1×2²+0×2¹+1×2⁰= 16+4+1= 21

10111₂ = 10111B = 1×2⁴+0×2³+1×2²+1×2¹+1×2⁰= 16+4+2+1= 23

100011₂ = 100011B = 1×2⁵+0×2⁴+0×2³+0×2²+1×2¹+1×2⁰=32+2+1= 35

Examples:

27₈ = 2×8¹+7×8⁰= 16+7 = 23

30₈ = 3×8¹+0×8⁰= 24

4307₈ = 4×8³+3×8²+0×8¹+7×8⁰= 2247

Decimal Numeral System - Base-10

Decimal numbers uses digits from 0..9.

These are the regular numbers that we use.

Example:

2538₁₀ = 2×10³+5×10²+3×10¹+8×10⁰

Examples:

28₁₆ = 28H = 2×16¹+8×16⁰= 40

2F₁₆ = 2FH = 2×16¹+15×16⁰= 47

BC12₁₆ = BC12H = 11×16³+12×16²+1×16¹+2×16⁰= 48146

Numeral systems conversion table

Decimal Base-10	Binary Base-2	Octal Base-8	Hexadecimal Base-16
0	0	0	0
1	1	1	1
2	10	2	2
3	11	3	3
4	100	4	4
5	101	5	5
6	110	6	6
7	111	7	7
8	1000	10	8
9	1001	11	9
10	1010	12	A
11	1011	13	B
12	1100	14	C
13	1101	15	D
14	1110	16	E
15	1111	17	F
16	10000	20	10
17	10001	21	11
18	10010	22	12
19	10011	23	13
20	10100	24	14
21	10101	25	15
22	10110	26	16
23	10111	27	17
24	11000	30	18
25	11001	31	19
26	11010	32	1A
27	11011	33	1B
28	11100	34	1C
29	11101	35	1D
30	11110	36	1E
31	11111	37	1F
32	100000	40	20

Detailed Chapter Notes - Number System, Class 9 Mathematics ...

Saturday, April 25, 2020

10 VEDIC MATHS TRICKS TO MAKE YOUR CALCULATION FASTER

10 VEDIC MATHS TRICKS TO MAKE YOUR CALCULATION FASTER

Tired of doing calculations
Ever lost marks due to silly mistakes??

Have you spent a looooooooong time calculating answer for a particular problem and still got it wrong.

Don't worry with these tricks your calculation will become easier

How to square a number whose last digit is 5

This vedic maths formula is pretty simple by which you can square any 2-digit number which has 5 in its one’s place.

First, multiply the 1st digit on the left-hand side with 1 and then,

write 25 at the end.

That’s trick 1 for you. You still didn’t get it.
See the example below: –

For example: (75) ² =?

Step 1:75 x 75 = …….25 (at the end)

Step 2:7x (7+1) = 7 x 8 = 56

Therefore, the answer is 5625.

https://youtu.be/cAVph17rWlE

2. Multiplication of a number with 5

Memorizing 5 table is every easy. But as the smaller numbers turn to larger numbers, calculation turns complex.

This vedic maths technique helps you to solve this problem.

Here, you have to take any number and divide it by 2.
If your result is a whole number,
then add 0 (zero digit) at the end of the number.
If it is not a whole number, then add 5 at the end and ignore whatever remainder

you have got.

For example: 8426 x 5 =?

Step 1: 8426 / 2 = 4213

Step 2: It is a whole number, so add 0

The answer will be 8426 x 5 = 42130

Let’s try another: 7337 x 5

Step 1:3773 / 2 = 3668.5

Step 2: This is a fractional number, so we will ignore remainder and add 5 at the end.
The answer will be 7337 x 5 = 36685

3. How to subtract a number from 1000, 10000, 100000 and so on.

This maths technique is very useful when you want accurate subtracted results from 1000, 10000, 100000 and so on……

There is only one formula – Subtract all the digits from 9 and last digit from 10.

For example: 1000 – 876 =?
We simply subtract each figure in 876 from 9 and the last figure from 10.

Step 1. 9 – 8 = 1

Step 2. 9 – 7 = 2

Step 3. 10 – 6 = 4

So, the answer is 1000 – 876 = 124

4. How to Multiply any 2-digit numbers between 11 to 19

This trick is of great help if you are just like me and cannot remember the tables after 10.
Once practiced for adequate amount of times, you can calculate the results very fast.
There are in total 4 steps to solve through this type of trick

Step 1: Add the unit digit of smaller number to the larger number.

Step 2: Multiply the sum result by 10.

Step 3: Multiply both number’s unit digit.

Step 4: Add both the numbers (which were involved in step 1 & step 2).

For example: Take 2 numbers like 12 and 15.

Step 1. 15 + 2 =17

Step 2. 17*10 = 170.

Step 3. 2*5 = 10

Step 4. Add the two numbers, 170+10 and the answer is 18

5. Division of a large number by 5

This technique quickly gives the answer
after division of any large number by 5.

There are only two steps which you need to follow.

First, being multiplication of number by 2 and

second being removal of digit after decimal point.

For example: 415 / 5 =?

Step 1. 415 * 2 = 207.5

Step 2. Move the decimal: 207.5 or just 207

6. How to Multiply any two-digit number with 11

Using this mental math trick, multiplication can be done swiftly.

To multiply 45 and 11,
let us imagine that there is a gap between 45
Step 1: Put an imaginary space in between: 45*11= 4_5

Step 2: Just add 4 and 5 and put the result in the imaginary space

So, the answer is: 45 * 11 = 495

Let’s try another number….

36 * 11 = 3 (3+6) 9 = 396

7. Multiplication of any large number by 12

In order to multiply any no. by 12
we need to just double the last digit of the number and then, double each digit and add it to its neighboring number.

For example: 3243 * 12 =?

Let’s break it into simple steps:
Step 1. 3243 * 12 = _____6 (Double of Last Digit 3= 6 )
Step 2. 3243 * 12 = ____16 (Now Double 4= 8, and add it to 3, 8+3=11, 1 will get carry over)

Step 3. 3243 * 12= ___916 (Now Double 2=4, and add it to 4 with carry, 4+4+1=9)

Step 4. 3243* 12= _8916 (Now Double 3=6, and add it to 2, 6+2=8)

Step 5. 3243 * 12= 38916

So your final answer of 3243 * 12 = 38916

8. Multiplication of any 3-digit numbers

Take any two numbers like 204 and 206

Step 1. Now subtract the number at unit place.

204-4=200

206-6=200

Step 2. Now select any no. and add the unit digit of another no.

204+6=210

Step 3. Now multiply, 210×200 = 42000

Step 4. Now multiply the unit digits of both numbers, 4×6=24

Step 5. Add, 42000+24 = 42024

The product of the numbers 204 and 206 is 42024

9. How to calculate square of any number

Calculating squares can be very easy if you are doing it using Vedic maths.

Step 1. Choose a base nearer to the no. whose sq. is to be found.

Step 2. Find the difference of the no. from its base.

Step 3. Add the difference with the no.

Step 4. Multiply the result with the base.

Step 5. Add the product of the sq. of the difference with the result of the above point.

Let’s take an example to understand this: (88) ² =?

Step 1. Choose 100 as base

Step 2. Difference =88-100 = -12

Step 3. Number + difference = 99 + (-12) = 87

Step 4. Multiplying result with base = 87*100 = 8700

Step 5. Adding result with square of difference= 8700 + (-12)² = 8844

10.